咨询客服

联系电话：

18562583552

QQ客服：

立即咨询

工作时间：

9:00 ~ 17:00 （工作日）

ZenDAS使用手册 更多
1. 安装ZenDAS
1.1. 环境搭建
1.1.1 搭建Ubuntu环境安装ZenDAS
1.1.2 搭建Centos环境安装ZenDAS
1.1.3 安装PHP的ioncube拓展
1.1.4 安装PHP的xlswriter拓展
1.2 开始安装
1.3 渠成命令行安装
2. 登录
2.1 账号登录
2.2 退出系统
3. 数据管理
3.1. 数据源
3.1.1 数据源列表
3.1.2 添加数据源
3.2. 数据表
3.2.1 原始表
3.2.2 中间表
3.2.3 创建中间表
4. 项目管理
4.1 浏览项目
4.2 创建分析项目
4.3 编辑项目
4.4 编辑项目权限
4.5 删除项目
4.6 切换项目
5. 分析报告
5.1 创建分析报告
5.2 重命名分析报告
5.3 删除分析报告
6. 分析过程管理
6.1 支持的分析方法
6.2 添加分析方法
6.3 修改分析方法参数
6.4 删除分析方法结果
6.5 更新分析结果
6.6 注释分析结果
6.7 复制分析结果
6.8 导出分析结果
7. 分析方法
7.1 五类分析方法
7.2. 图形
7.2.1 箱线图
7.3. 相关与回归
7.3.1 Gompertz
7.3.2 相关性
7.3.3 回归拟合图
7.3.4 线性回归
7.3.5 多次方程回归
7.4. 控制图
7.4.1 I-MR控制图
7.5. 假设检验
7.5.1 正态性检验
7.6. 统计
7.6.1 基本统计量
7.6.2 蒙特卡罗模拟
8. 用户管理
8.1 浏览用户
8.2 添加用户
8.3 编辑用户
8.4 删除用户
9. 个性化设置
9.1 个人信息维护
9.2 切换界面语言
10. 系统信息
10.1 版本信息
10.2 帮助中心
10.3 访问官网

线性回归

2025-04-23 17:11:04
ZenDAS
45
最后编辑：张玉洁 于 2025-04-24 16:53:39
分享链接
摘要：线性回归是一种统计分析方法，用于研究自变量（X）与因变量（Y）之间的线性关系。支持线性拟合，用户可以选择一个或多个字段作为 X 轴，并指定一个字段作为 Y 轴。分析结果包括回归方程、系数、模型汇总数据、方差分析、异常值诊断和残差图。

1. 分析方法简介

线性回归是一种统计分析方法，用于研究自变量（X）与因变量（Y）之间的线性关系。支持线性拟合，用户可以选择一个或多个字段作为 X 轴，并指定一个字段作为 Y 轴。分析结果包括回归方程、系数、模型汇总数据、方差分析、异常值诊断和残差图。

2. 输入数据要求

在使用线性回归分析功能前，请确保数据满足以下要求：

  • X 和 Y 字段应为数值类型（连续变量）。
  • 数据应尽量避免缺失值或极端异常值，以确保分析结果的准确性。
  • 建议样本量足够大，以确保模型稳定性和可靠性。
  • 数据应满足独立性假设，即观测值之间相互独立。

3. 输出结果解释

线性回归分析完成后，软件会生成以下结果：

3.1 回归方程

回归方程表示自变量（X）与因变量（Y）之间的数学关系。方程形式为：

Y = β 0 + β 1X 1 + β 2X 2 + ... + ε

其中， β 0是截距， β 1, β 2, ... 是回归系数，ε 是误差项。

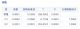
3.2 系数表

项 系数 系数标准误 T 值 P 值 方差膨胀因子
截距 β 0 截距的标准误 截距的 T 值 截距的 P 值 -
X 1 β 1 X 1 的标准误 X 1 的 T 值 X 1 的 P 值 VIF 1
  • 系数：表示自变量对因变量的影响大小。
  • 系数标准误：衡量系数的稳定性，标准误越小，系数越可靠。
  • T 值：用于检验系数的显著性，T 值绝对值越大，系数越显著。
  • P 值：表示系数是否显著。通常 p < 0.05 说明系数显著。
  • 方差膨胀因子（VIF）：用于检测自变量之间的多重共线性。VIF 值大于 10 表明存在严重的多重共线性问题。

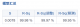
3.3 模型汇总数据

模型汇总数据包括以下指标：

  • 标准误差S：表示模型的预测精度，越小越好。
  • 决定系数R²：表示模型解释的变异比例，范围 0 到 1，越大越好。
  • 调整 R²：考虑自变量数量后的 R²，更适用于多元回归。

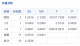
3.4 方差分析（ANOVA）

方差分析用于检验模型的显著性：

3.4.1. 自由度（df, Degrees of Freedom）

定义：自由度表示数据中可以自由变动的独立信息量。

分类：

  • 回归自由度（df回归）：等于自变量的个数（k）。表示模型中自变量的数量。
  • 残差自由度（df残差）：等于样本量减去自变量个数再减1（n - k - 1）。表示模型中无法解释的部分的独立信息量。
  • 总自由度（df总）：等于样本量减1（n - 1）。表示数据中总的独立信息量。

3.4.2. 平方和（SS, Sum of Squares）

定义：平方和表示数据点与均值或预测值之间的差异的平方和，用于衡量变异的大小。

分类：

  • 回归平方和（SS回归）：表示回归模型能够解释的变异部分。
  • 残差平方和（SS残差）：表示回归模型无法解释的变异部分。
  • 总平方和（SS总）：表示数据中总的变异。

3.4.3. 均方（MS, Mean Square）

定义：均方是平方和除以自由度，用于标准化变异的大小。

分类：

  • 回归均方（MS回归）：表示回归模型中每单位自由度的变异。
  • 残差均方（MS残差）：表示残差中每单位自由度的变异。

3.4.4. F值（F Statistic）

定义：F值用于检验回归模型的显著性，通过比较回归均方和残差均方来判断自变量是否对因变量有显著影响。

含义：

  • F值越大，说明回归模型越显著，自变量对因变量的影响越大。
  • F值越小，说明回归模型不显著，自变量对因变量的影响可能不显著。

3.4.5. P值（P-value）

定义：P值表示在假设回归模型不显著（即自变量对因变量无影响）的情况下，观察到当前F值（或更大）的概率。

取值范围：0 到 1。

含义：

  • 通常以 0.05 作为显著性水平。
  • 如果p < 0.05，说明回归模型显著，自变量对因变量有显著影响。
  • 如果p ≥ 0.05，说明回归模型不显著，自变量对因变量的影响可能不显著。

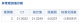
3.5 异常值诊断

系统会识别数据中的异常值，并提供其位置和影响程度，帮助用户判断是否需要处理这些异常数据。

3.6 残差图

  • 残差的正态概率图：检查残差是否服从正态分布。
  • 残差与拟合值图：检查残差是否随机分布，是否存在异方差性。
  • 残差频率的直方图：直观展示残差的分布情况。
  • 残差与观测值顺序图：检查残差是否存在时间或顺序上的相关性。

4. 使用步骤

  1. 选择“线性回归”分析方法。
  2. 选择 X 轴字段（可多选）和 Y 轴字段。
  3. 点击“保存”按钮。
  4. 查看并解读输出结果。

5. 注意事项

  • 确保数据满足线性回归的假设（线性、独立性、正态性、同方差性）。
  • 如果模型拟合不佳，尝试增加变量或对数据进行变换。
  • 异常值可能对回归结果产生较大影响，建议根据实际情况决定是否处理。